도입
이 자그마한 튜토리얼은 3D와 2D에 유용한 벡터 수학의 짧고 실용적인 소개를 하는 것이 목표입니다. 다시, 벡터 수학은 3D 뿐만 아니라 2D 게임에도 유용합니다. 여러분이 한 번만 잡아두면 복잡한 행동도 더욱 쉽게 프로그래밍 하게 해주는 놀라운 도구가 됩니다.
종종 젊은 프로그래머들이 2D 게임의 벡터 수학 대신 삼각 함수를 사용하는 것과 같이, 광범위한 문제를 해결하기 위해 잘못된 수학에 너무 많이 의존하게 되는 경우가 있습니다.
이 튜토리얼은 즉시 게임의 예술에 적용 가능한 실용적인 부분에 초점을 맞추었습니다.
좌표 시스템 (2D)
전통적으로, 좌표는 x는 수평값을 그리고 y는 수직값을 지니는 (x, y)의 한 쌍으로 정의합니다. 주어진 스크린이 2차원의 사각형인 경우에만 이것이 성립합니다. 한 예로 2D 공간의 위치입니다 :
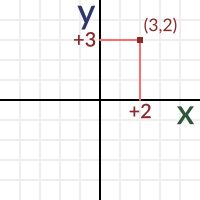
위치는 공간의 어디도 될 수 있습니다. (0, 0)은 원점이라는 이름이 있다. 이 용어는 나중에 암시적으로 사용이 되므로 잘 기억해두세요. n차원의 좌표 시스템의 (0, 0)은 원점입니다.
벡터 수학에서, 좌표는 두 개의 다른 사용법이 존재하며, 둘 다 동일하게 중요합니다. 이들은 위치뿐만 아니라 벡터도 대표합니다. 벡터라고 상상했을 때, 이전과 동일한 위치는 다른 의미를 갖습니다.
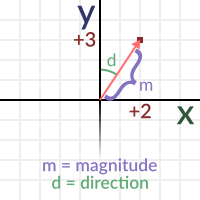
벡터라고 상상했을 때, 방향과 크기의 두 속성이 추론 가능합니다. 공간의 모든 위치는 원점을 제외하고는 벡터가 될 수 있습니다. 이것이 좌표 (0, 0)이 방향을 대표할 수 없는 이유입니다 (크기도 0).

방향
방향은 간단하게 벡터 지점이 어디를 가리키고 있는 지를 나타냅니다. 화살이 원점에서 시작되었고 [목표:위치]를 향해 날아간다고 상상하세요. 화살의 끝은 위치이며, 언제나 원점에서 멀어지는 쪽을 바깥으로 지닙니다. 벡터를 화살로 생각하는 것은 꽤 도움이 됩니다.

크기
최종으로, 벡터의 길이는 원점에서 지점까지의 거리입니다. 벡터의 길이를 쉽게 얻는 방법은 피타고라스 정의를 쓰는 것입니다.
var len = sqrt( x*x + y*y )
하지만... 각도는요?
왜 각도를 쓰지 않는 건가요? 아무튼, 우리는 벡터를 방향와 크기가 아니라 각도와 크기로도 생각할 수 있습니다. 각도도 익숙한 개념이죠.
솔직히 말해서, 그리고 대부분의 시간에 직접 다루어지지 않으며 각도는 벡터 수학에서 크게 유용하지 않습니다. 2D에서는 먹힐 지 모르지만 3D에서는 보통 각도로 할 수 있는 많은 일들은 쓸모가 없습니다.
아직도, 각도를 사용하는 것은 2D에서도 이유가 되지 않습니다. 2D에서 각도로 할 수 있는 많은 일들이 벡터 수학을 사용하면 더욱 자연스럽고 쉽게 할 수 있습니다. 그러니, 삼각법은 놓아주고, 벡터를 수용할 준비를 하세요! 어떠한 경우에도 벡터로부터 각도를 얻는 것은 쉽고 trig..er로 수행할 수 있습니다. 아 이게 뭐죠? 제 말은 atan2() 함수를 말한거에요.
고도에서의 벡터
# create a vector with coordinates (2,5) var a = Vector2(2,5) # create a vector and assign x and y manually var b = Vector2() b.x = 7 b.y = 8
벡터와 함께 작업할 때에는 멤버에 직접 수행할 필요가 없습니다(사실 이게 더 느립니다). 벡터는 일반적인 산술적 연산도 지원합니다 :
# add a and b var c = a + b # will result in c vector, with value (9,13)
이건 아래와 같은 작업입니다 :
var c = Vector2() c.x = a.x + b.x c.y = a.y + b.y
전의 방법이 더 효율적이고 읽기도 편합니다.
덧셈이나 뺄셈, 곱셈, 나눗셈 같이 일반적인 산술 연산도 지원합니다.
벡터의 곱셈과 나눗셈은 스칼라라고 부르는 단일 숫자와 혼합해서 쓸 수 있습니다
# multiplication of vector by scalar var c = a*2.0 # will result in c vector, with value (4,10)
아래와 같은 작업입니다 :
var c = Vector2() c.x = a.x*2.0 c.y = a.y*2.0
다시 한 번 말하지만 앞의 방법이 더 효율적이고 가독성이 좋습니다.
수직 벡터
2D 벡터를 왼쪽 혹은 오른쪽으로 90도 돌리는 것은 정말 쉽습니다. x와 y만 바꾸고 x와 y를 부정하면 됩니다. (회전 방향은 부정된 방향에 따라 달라집니다.)
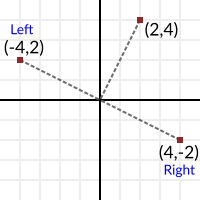
예시 :
var v = Vector2(0,1) # rotate right (clockwise) var v_right = Vector2(v.y, -v.x) # rotate left (counter-clockwise) var v_left = Vector2(-v.y, v.x)
이건 자주 사용하는 간단한 속임수입니다. 3D 벡터로는 할 수 없는데 왜냐하면 무한한 값의 수직 벡터가 존재하기 때문입니다.
단위 벡터
좋아요, 우린 이제 벡터가 무엇인지 알았습니다. 벡터는 방향과 크기를 가지고 있죠. 우리는 고도에서 이들을 어떻게 써야하는지도 알고있습니다. 다음 단계는 단위 벡터에 대해 배우는 것입니다. 2D에서는 반지름으로 원을 그리는 것을 상상하세요. 원은 2차원에 존재하는 모든 단위 벡터를 포함합니다.
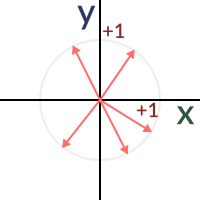
그러면, 단위 벡터는 무엇이 그렇게 특출난걸까요? 단위 벡터는 놀랍습니다. 다르게 말하자면, 단위 벡터는 여러, 매우 유용한 속성을 가지고 있다는 뜻이죠.
표준화
방향을 그대로 가지고 어떤 벡터이든 크기를 1.0으로 줄이는 것을 표준화라고 합니다. 표준화는 벡터의 x와 y (3D에서는 z까지) 요소를 그 크기로 나누면 수행됩니다.
var a = Vector2(2,4) var m = sqrt(a.x*a.x + a.y*a.y) a.x /= m a.y /= m
여러분이 추측하셨을 수도 있는데, 벡터가 0의 크기를 가질 때(즉, 벡터는 아니지만 원점을 null 벡터라고도 함), 0으로 나누는 경우가 발생하고 역극성을 제외하고 우주는 두번째 빅뱅을 겪습니다. 그리고 다시 되돌아옵니다. 결과적으로 인간적으로는 안전하지만 고도는 에러를 출력합니다. 기억하세요!! Vector(0,0)은 표준화 할 수 없습니다.
물론, Vector2와 Vector3 모두 이에 대한 메소드가 있습니다 :
a = a.normalized()
점곱 (Dot Product)
좋아요, 점곱은 벡터 수학에서 가장 중요한 부분입니다. 점곱 없이는, 퀘이크는 만들어지지도 않았을 것입니다. 이 튜토리얼에서 가장 중요한 부분이며, 확실하게 잡아두세요. 많은 사람이 벡터 수학을 이 부분을 이해하려다 포기합니다. 매우 간단하지만 말예요. 그 사람들은 머리나 꼬리를 만들 수 없습니다. 왜냐구요? 왜냐하면...
점곱은 두 벡터로 스칼라를 반환합니다.
var s = a.x*b.x + a.y*b.y
예, 그렇습니다. 벡터 a의 x에 벡터 b의 x를 곱합니다. y에도 똑같이 해주시고 더해주세요. 3D는 아래와 같겠죠 :
var s = a.x*b.x + a.y*b.y + a.z*b.z
저도 이게 정말 의미없다는 것을 알고있습니다! 여러분은 내장 함수를 이용해 이렇게도 할 수 있습니다 :
var s = a.dot(b)
두 벡터의 순서는 a.dot(b)이던 b.dot(a)이던 같은 값을 반환합니다. 여기서 절망이 시작되며 책과 자습서에서 다음과 같은 공식을 보여줍니다.
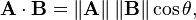
3D 게임이나 복잡한 2D 게임을 포기할 시간이 되었다고 깨닫는 시간입니다. 어떻게 간단한 것이 이렇게 복잡하게 될 수 있죠? 누군가는 다음 젤다와 콜 오브 듀티를 만들 겁니다. 탑 다운 RPG는 결국 그렇게 나빠보이지 않는데요. 네, 저는 스팀에서 누군가가 저렇게 말하는 것을 들었습니다.
이게 여러분이 빛날 순간입니다. 포기하지 마세요! 이 지점에서 이 튜토리얼은 튜토리얼은 빠른 회전을 하며 점곱을 유용하게 만드는 것에 초점을 맞춥니다. 이제 이게 왜 유용한지입니다. 우리는 점곱의 실생활에서의 용례에 집중할 겁니다. 더 이상의 공식은 없습니다. 공식은 여러분이 그게 어디에 한 번 어디에 유용한 지 알게되면 말이 될 것입니다.
측선
처음으로 점곱의 속성이 유용하고 중요한 것은 옆에 어떤 것이 있는지 볼 때입니다. 두 벡터 a와 b가 있다고 상상해봅시다. 어떤 방향와 크기도 좋습니다(원점만 빼구요). 그들이 무엇인지 신경 쓰지말고 우리가 그들 사이의 점곱을 한다고 상상해보세요.
var s = a.dot(b)
이 작업은 단일 부동소수점 번호를 반환합니다. (하지만 우리가 벡터 세계에 있기 때문에 스칼라라고 부르는 용어를 계속 사용할 겁니다) 이 번호는 다음과 같은 내용을 말해줍니다 :
- 번호가 0보다 크면, 둘 다 같은 방향을 보고 있는 것입니다. (둘의 각도가 90도 이하)
- 번호가 0보다 작으면 서로 반대 방향을 보고 있는 것입니다. (둘의 각도가 90도 이상)
- 만약 숫자가 0이면 벡터는 L의 형태를 지니는 것입니다. (둘의 각도가 90도)

실제 사용 시나리오에 대해 생각해봅시다. 뱀이 숲을 지나가는데, 적이 근처에 있습니다. 어떻게 적이 뱀을 발견했다고 빠르게 말해 줄 수 있을까요? 그를 발견하기 위해서는, 적들이 뱀을 볼 수 있어야 합니다. 다음과 같은 경우를 가정해봅시다 :
- 뱀은 위치 A에 있습니다
- 적은 위치 B에 있습니다.
- 적은 F 방향을 보고 있습니다.
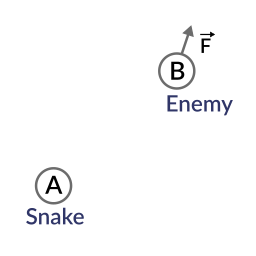
var BA = A - B
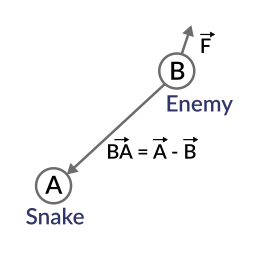
이상적으로 만약 적군이 뱀을 보고 있었다면, 눈을 마주치기 위해서, 벡터 BA와 동일한 방향으로 할 겁니다.
만약 F와 BA의 점곱이 0보다 크면, 뱀이 발견되는 겁니다. 이는 적군이 뱀을 향해 마주하고 있다는 것을 우리가 알 수 있기 때문입니다.
if (BA.dot(F) > 0): print("!")
지금까지 뱀은 안전한 것 같네요.
단위 벡터와 측선
자, 이제 두 벡터 사이의 점곱이 우리에게 그들이 같은 쪽을 보고있는지, 반대쪽을 보고있는지 아니면 서로 수직을 이루는지를 알려주는 지를 알 수 있게 되었습니다.
이 기능은 모든 벡터에 대해 동일하게 작동하며, 크기에 관계 없이 단위 벡터도 예외가 아닙니다. 그러나 단위 벡터의 동일한 속성을 사용하면 추가적인 속성이 추가되므로 훨씬 더 흥미로운 결과를 얻을 수 있습니다.
- 두 벡터가 정확하게 동일한 방향을 향해 서 있는 경우 (서로 평행하면, 그 사이의 각도는 0도), 결과 스칼라는 1이다.
- 두 벡터가 정확하게 반대 방향을 향해 있는 경우 (서로 평행하지만 그들 사이의 각도가 180도인 경우), 결과 스칼라는 -1이다.
- 만약 두 사이각이 0도이면, 점곱은 1이다.
- 만약 두 사이각이 90도이면, 점곱은 0이다.
- 만약 두 사이각이 180도이면, 점곱은 -1이다.
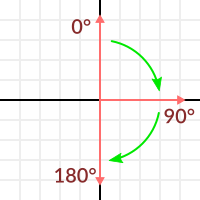
결과 스칼라를 그리면서요!
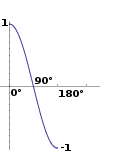
아하! 이제 알겠습니다. 이건 코사인 함수에요!
그러면 대개....
두 단위 벡터 사이의 점곱은 두 벡터 사이각의 코사인입니다. 두 벡터간의 각도를 구하려면 다음을 수행해야 합니다 :
var angle_in_radians = acos( a.dot(b) )
대체 이게 무슨 쓸모가 있을까요? 각도를 직접 얻는 것은 아마 그만큼 유용하지 않겠지만, 각도를 말할 수 있는 것만으로 참조를 위해 유용합니다. 키네마틱 캐릭터 데모의 한 예입니다, 캐릭터가 특정 망향으로 움직이면 우리는 오브젝트를 때리는 겁니다. 바닥에 부딪힌 게 맞는지 어떻게 알 수 있죠?
부딪힌 부분과 우리가 전에 계산했던 각도를 비교함으로 알 수 있습니다.
이 코드의 장점은 동일한 코드가 정확히 동일하게 동작하고 3D에서 수정이 필요하지 않다는 것입니다. 벡터 수학은 대부분 치수 독립적이므로 축을 추가하거나 제거할 때 복잡성이 거의 추가되지 않습니다.
평면
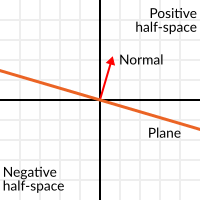
표면에 수직인 단위 벡터(즉, 표면의 방향을 설명함)를 단위 표준 벡터라고 합니다. 그렇지만 보통 줄여서 *정상(normals)이라고 합니다. 평면, 3D 형상(각 면이나 정점이 선으로 된 위치를 결정하기 위해) 등에 표준이 나타납니다. 정상은 단위 벡터이지만 그 용도 때문에 정상이라고 합니다. (우리가 원점을 (0, 0)이라고 부루는 것처럼!)
보이는 것 만큼 간단합니다. 평면은 원점을 통과하며 평면의 표면은 단위 벡터(혹은 정상)와 수직을 이룹니다. 벡터를 향해 있는 측면은 양의 절반 공간이고, 다른 쪽은 음의 절반 공간입니다. 3D에서는 평면이 한 줄 대신 무한한 표면(방향을 설정하고 원점에 고정할 수 있는 무한하고 평평한 종이)이라는 점을 제외하고는 정확히 동일합니다.
평면까지의 거리
var distance = normal.dot(point)
하지만 절대 거리뿐만이 아니라, 점이 음의 절반의 공간에 있는 경우에도 거리는 음수가 됩니다.
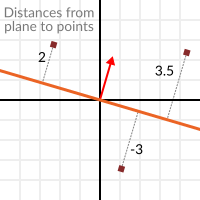
이를 통해 평면의 어느 쪽에 점이 있는지 알 수 있습니다.
원점으로부터의 거리
여러분이 어떤 생각을 하는지 알고 있습니다! 현재까지는 괜찮지만, 실제 평면은 원점을 지날 뿐 아니라 공간의 어디에도 있습니다. 여러분은 실제 평면 행동을 지금 당장 원하실 겁니다.
평면이 공간을 둘로 나눌 뿐만 아니라, 극성도 띕니다. 이는 완벽하게 중첩된 평면을 갖는 것이 가능하다는 것을 의미하지만, 이드르이 음과 양의 공간은 서로 뒤바뀌었습니다.
이 점을 염두에 두고, 전체 평면을 정상적인 N으로 설명하고 스칼라 D로부터 떨어져 있는 거리를 표현해보죠. 따라서 우리 평면은 N와 D로 표시됩니다.
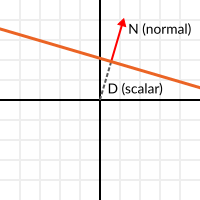
3D 수학을 위해 고도는 이를 다루기 위한 자체 타입인 평면을 제공합니다.
기본적으로, N과 D는 2D와 3D(N 차원에 따라 다름)를 위해 공간의 어느 평면도 대표할 수 있으며, 연산은 두 평면에서 동일합니다. 전과 동일하지만, D는 원점에서 출발해 N쪽 평면 방향으로 갑니다. 예를 들어, 점의 평면에 닿고싶다면 이렇게 하세요 :
var point_in_plane = N*D
그러면 정상 벡터가 늘어나고 (크기가 조정되므로) 평면에 닿게 됩니다. 이 수학은 헷갈릴 수도 있지만 보기보다 간단합니다. 다시 한번 점에서 평면까지의 거리를 알고 싶은 경우, 거리 조정을 제외하고는 동일한 작업을 수행합니다 :
var distance = N.dot(point) - D
같은 작업을 내장 함수로 할 수 있습니다 :
var distance = plane.distance_to(point)
다시 말해서, 양의 거리 또는 음의 거리를 반환합니다.
평면의 극성을 뒤집는 것도 매우 간단하며, N과 D를 모두 부정하면 됩니다. 결과적으로 평면은 동일한 위치에 있지만 반전된 음과 양의 절반 공간으로 이어집니다 :
N = -N D = -D
물론 고도는 평면에서도 이 연산자를 실행하며 다음을 수행합니다 :
var inverted_plane = -plane
기대한 대로 작동할 겁니다.
기억하세요 평면은 단지 평면과의 거리를 계산하는 것이 주로 실용적인 일입니다. 그렇다면 점에서 평면까지의 거리를 계산하는 것이 왜 유용할까요? 그건 정말 극도로 유용합니다! 간단한 예를 몇가지 보죠.
2D에서의 평면 구성
평면이 갑자기 나타나는 것이 분명하지 않아서, 평면을 만들어야 합니다. 2D로 이들을 만드는 것은 쉬우면, 이는 정상 (단위 벡터)와 한 점 또는 공간의 두 점에서 이루어질 수 있다.
정상(단위 벡터)과 점의 경우 대부분의 작업은 이미 단위 벡터가 계산됨으로 끝나므로 단위 벡터와 점의 점곱으로 D를 계산하면 된다.
var N = normal var D = normal.dot(point)
공간의 두 지점에서 같은 공간을 공유하지만 반대 방향을 가리키는 두 개의 평면이 실제로 지나가고 있습니다. 두 지점에서 정상적으로 계산하려면 먼저 방향 벡터를 확보한 다음 양쪽으로 90도 회전해야 합니다.
# calculate vector from a to b var dvec = (point_b - point_a).normalized() # rotate 90 degrees var normal = Vector2(dvec.y,-dev.x) # or alternatively # var normal = Vector2(-dvec.y,dev.x) # depending the desired side of the normal
나머지는 앞의 예시와 동일한 수준이므로, 점 _a 또는 점 _b 중 하나가 작동합니다.
var N = normal var D = normal.dot(point_a) # this works the same # var D = normal.dot(point_b)
3D로 동일한 작업을 수행하는 것은 약간 더 복잡하고 추가적으로 설명될 것입니다.
평면의 몇가지 예
여기 평면이 무엇에 유용한지에 대한 간단한 예가 있습니다. 여러분이 볼록한 다각형을 가지고 있다고 상상해보세요. 예를 들어 사각형, 사다리꼴, 삼각형 또는 안쪽으로 굽지 않은 면이 있는 다각형 등이 있습니다.
다각형의 모든 세그먼트에 대해 해당 세그먼트를 통과하는 평면을 계산합니다. 평면의 목록을 만들면 예를 들어 점이 다각형 안에 있는 지 확인하는 등의 깔끔한 작업을 수행할 수 있습니다.
모든 평면을 통과해 점에 대한 거리가 양의 값을 가진 평면을 찾을 수 있다면 점은 다각형 외부에 있는 것입니다. 그렇게 할 수 없다면 점이 안에 있다는 것입니다.
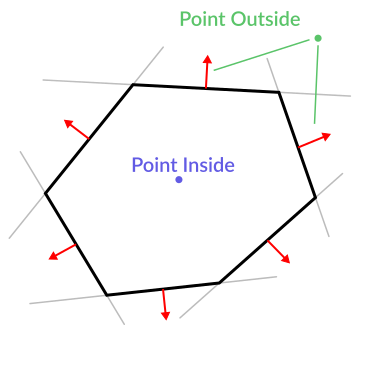
코드는 이런 식입니다 :
var inside = true for p in planes: # check if distance to plane is positive if (N.dot(point) - D > 0): inside = false break # with one that fails, it's enough
꽤 멋지죠? 하지만 더 나아질 수 있습니다! 조금 더 노력하면 비슷한 논리가 두 개의 볼록한 다각형들도 발견하게 해줍니다. 이를 분리 축 이론(또는 SAT)이라고 하며, 물리학적 엔진의 대부분은 충돌을 감지하기 위해 이를 사용합니다.
아이디어는 굉장히 간단합니다! 점으로 평면이 양의 거리를 반환하는 것을 확인하는 것 만으로도 점이 바깥에 있는지를 알 수 있습니다. 다른 다각형을 사용하는 경우, **다른* 다각형 점*이 양의 거리를 반환하는 평면을 찾아야합니다. 이 점검은 A의 평면에서 B의 점을 기준으로 수행되며, B의 평면에서 A의 점을 기준으로 수행됩니다 :
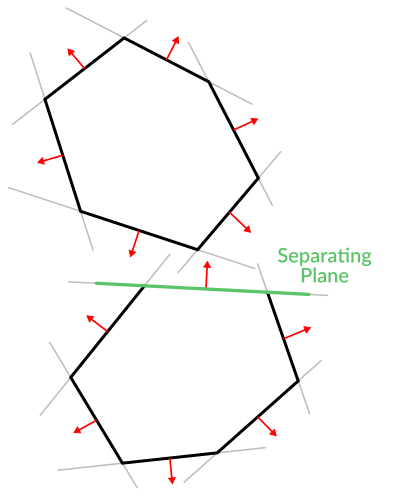
코드는 다음과 같습니다 :
var overlapping = true for p in planes_of_A: var all_out = true for v in points_of_B: if (p.distance_to(v) < 0): all_out = false break if (all_out): # a separating plane was found # do not continue testing overlapping = false break if (overlapping): # only do this check if no separating plane # was found in planes of A for p in planes_of_B: var all_out = true for v in points_of_A: if (p.distance_to(v) < 0): all_out = false break if (all_out): overlapping = false break if (overlapping): print("Polygons Collided!")
여러분이 볼 수 있듯이, 평면은 꽤나 유용하며 이는 빙산의 일각입니다. 여러분은 아마도 볼록하지 않은 다각형에 대해서는 어떤 일이 일어나는지 궁금할 겁니다. 이것은 대개 오목 다가각형을 더 작은 볼록 다각형으로 분할하거나 BSP와 같은 기술을 사용(요즘은 사용하지 않는)하여 처리합니다.
벡터곱
점곱으로 꽤 많은 것을 할 수 있습니다! 하지만 벡터곱 없이는 파티가 완성되지 못합니다. 이 튜토리얼의 처음 부분을 기억하세요? 구체적으로 x와 y를 교환하여 수직(90도를 돌린) 벡터를 얻고 그 다음에 오른쪽(시계 방향) 또는 왼쪽(시계 반대 방향) 회전을 위해 두 벡터 중 하나를 제거하는 방법은 무엇일까요? 이는 결국 두 지점에서 정상적인 2D 평면을 계산하는 데 유용합니다.
앞서 언급한 것처럼 3D 벡터에는 무한한 수직 벡터가 있기 때문에 3D에는 이와 같은 것이 없습니다. 대신 세 점이 필요하므로 두 점에서 3D 평면을 얻는 것도 의미가 없습니다.
이런 종류의 일을 돕기 위해서, 인류의 최고 수학자들이 우리에게 벡터곱을 가져다 주었습니다.
벡터곱은 두 개의 벡터를 사용하여 또 다른 벡터를 반환합니다. 반환되는 세번째 벡터는 항상 첫번째 두 개에 수직입니다. 물론 소스 벡터는 동일하지 않아야하며 평행 또는 반대일 수 없습니다. 그렇지 않으면 결과 벡터는 (0, 0, 0)과 같습니다.
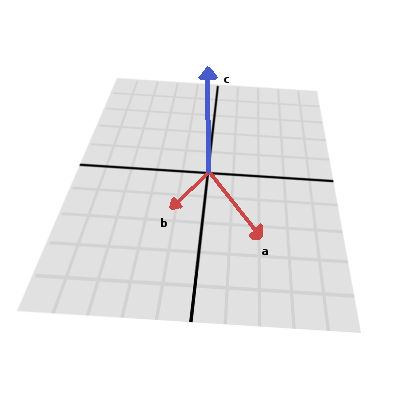
벡터곱의 공식은 다음과 같습니다 :
var c = Vector3() c.x = (a.y * b.z) - (a.z * b.y) c.y = (a.z * b.x) - (a.x * b.z) c.z = (a.x * b.y) - (a.y * b.x)
고도에서는 간단히 해서 :
var c = a.cross(b)
하지만 점곱과 달리, a.cross(b)와 b.cross(a)를 수행하면 서로 다른 결과가 나옵니다. 특히, 반환된 벡터는 두번째 경우에 부정됩니다. 여러분도 알고 있듯이, 이는 2D로 수직 벡터를 만드는 것과 일치합니다. 3D에서는 2D 벡터 쌍에 사용할 수 있는 두 개의 수직 벡터도 있습니다. 또한 두 단위 벡터의 벡터곱 결과는 단위 벡터가 아닙니다. 결과는 다시 표준화할 필요가 있습니다.
삼각형의 영역
벡터곱을 사용하여 3D 삼각형의 표면적을 얻을 수 있습니다. 주어진 삼각형은 A, B, C의 세 점으로 구성됩니다.
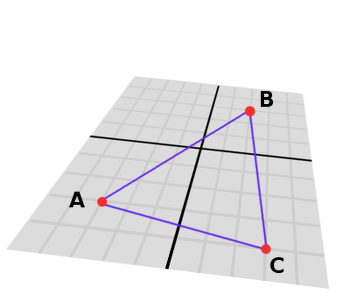
세 점 중 어떤 것이든 피벗으로 선택하고 다른 두 지점에 대한 주변 벡터를 계산합니다. 예를 들어, B를 피벗으로 사용합니다 :
var BA = A - B var BC = C - B
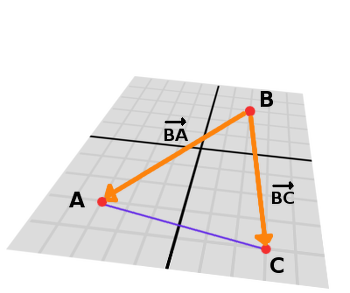
BA와 BC 사이의 벡터곱을 계산하여 수직 벡터 P를 얻을 수 있습니다 :
var P = BA.cross(BC)
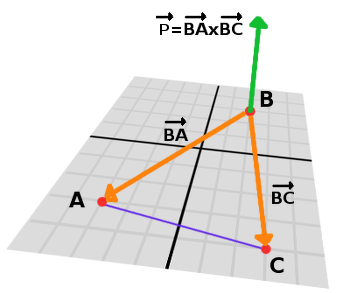
P의 길이(크기)는 두 벡터 BA오 ㅏBC에 의해 구축된 평행사변형의 표면적이므로, 삼각형의 표면적은 그 절반이다.
var area = P.length()/2
삼각 평면
P를 이전 단계에서 계산한 경우, 평면의 단위 벡터를 얻기 위해 이를 표준화합니다.
var N = P.normalized()
그리고 ABC 삼각형의 세 점 중 어느 곳이든 P 점곱을 사용하여 거리를 구합니다.
var D = P.dot(A)
환상적입니다! 삼각형으로 평면을 계산하셨습니다!
유용한 정보를 드리죠 (고도 소스 코드에서 찾을 수 있는 부분입니다). 삼각형에서 평면을 계산하면 2개의 평면이 생성될 수 있으므로 일종의 규칙을 설정해야 합니다. 이는 대게 삼각형의 앞면을 사용하는 것에 따라 달라집니다 (비디오 게임과 3D 시각화에서).
고도에서, 정면을 향하는 삼각형은 카메라를 보면, 시계 방향으로 배열되어 있는 삼각형들입니다. 카메라를 볼 때 시계 반대 방향으로 보는 삼각형은 그려지지 않습니다 (이렇게 하면 더 적게 그리는 데 도움이 되므로 물체의 뒷부분은 그려지지 않습니다).
좀 더 명확하게 하귀 위해, 아래 그림에서 삼각형 ABC는 전면 카메라에서 바라볼 때 시계 방향으로 보이지만, 후면 카메라에서는 시계 반대 방향으로 나타나므로 그려지지 않습니다.
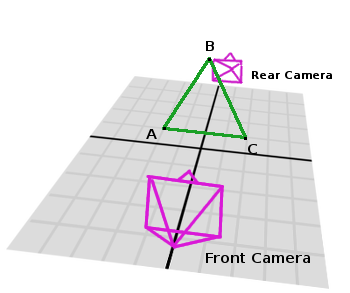
삼각형의 단위 벡터는 종종 그들이 볼 수 있는 방향으로 기울어지기 때문에, 이 경우에는 ABC라는 삼각형의 단위 벡터가 정면 카메라를 가리킵니다.
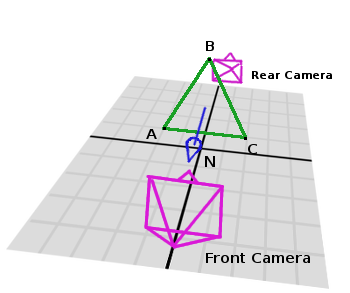
그래서, N을 얻기 위한 정확한 공식은 :
# clockwise normal from triangle formula var N = (A-C).cross(A-B).normalized() # for counter-clockwise: # var N = (A-B).cross(A-C).normalized() var D = N.dot(A)
3D에서의 충돌 감지
이는 또 다른 약간의 보너스입니다. 인내심을 갖고 이 긴 튜토리얼을 따라오는 것에 대한 보상입니다. 여기 또 다른 약간의 지혜가 있습니다. 직접 사용하는 경우(고도는 이미 충돌 감지를 꽤 잘합니다)는 아닐 수 있지만, 물리학적 엔진과 충돌 감지 라이브러리는 거의 다음과 같이 사용되기 때문에 이해하기에 매우 유용합니다 :)
2D에서 볼록한 형태를 2D 평면 배열로 변환하면 충돌 감지에 유용하다는 점을 기억하나요? 점이 볼록한 모양 안에 있는지 또는 2D의 볼록한 보양 두 개가가 중복되고 있는지를 검출할 수 있습니다.
자, 이것은 3D에서도 작동합니다. 만약 두 개의 3D 다면체 모양이 충돌한다면 분리된 평면을 찾을 수 없을 것입니다. 분리된 평면이 발견되면 모양이 분명히 충돌하지 않을 수 있습니다.
약간 새로 고치려면 다각형 A의 모든 수직면이 평면의 한 쪽에 있고 다각형 B의 모든 수직면이 반대쪽에 있음을 의미합니다. 이 평면은 항상 다각형 A 또는 다각형 B의 단면 중 하나입니다.
하지만 3D에서는 이 접근 방식에 문제가 있습니다. 분리 평면을 찾을 수 없는 경우도 있기 때문입니다. 이 상황에 대한 예입니다 :
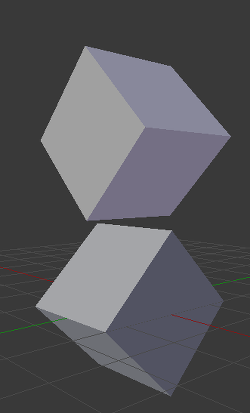
이를 방지하기 위해 일부 추가 평면을 분리자로 테스트해야합니다. 이러한 평면은 다각형 A의 가장자리와 다각형 B의 가장자리의 벡터곱입니다.
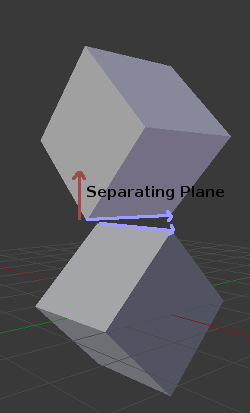
최종 알고리즘은 다음과 같습니다 :
var overlapping = true for p in planes_of_A: var all_out = true for v in points_of_B: if (p.distance_to(v) < 0): all_out = false break if (all_out): # a separating plane was found # do not continue testing overlapping = false break if (overlapping): # only do this check if no separating plane # was found in planes of A for p in planes_of_B: var all_out = true for v in points_of_A: if (p.distance_to(v) < 0): all_out = false break if (all_out): overlapping = false break if (overlapping): for ea in edges_of_A: for eb in edges_of_B: var n = ea.cross(eb) if (n.length() == 0): continue var max_A = -1e20 # tiny number var min_A = 1e20 # huge number # we are using the dot product directly # so we can map a maximum and minimum range # for each polygon, then check if they # overlap. for v in points_of_A: var d = n.dot(v) if (d > max_A): max_A = d if (d < min_A): min_A = d var max_B = -1e20 # tiny number var min_B = 1e20 # huge number for v in points_of_B: var d = n.dot(v) if (d > max_B): max_B = d if (d < min_B): min_B = d if (min_A > max_B or min_B > max_A): # not overlapping! overlapping = false break if (not overlapping): break if (overlapping): print("Polygons collided!")
이게 전부입니다! 도움이 되었기를 바라며, 이 튜토리얼의 내용이 명확하지 않다면 피드백을 주시고 알려주세요! 이제 다음 도전을 준비하셔야 할겁니다. 행렬과 변환입니다!
'레퍼런스 > 고도엔진' 카테고리의 다른 글
| 고도엔진 튜토리얼 #19 뷰포트와 캔버스 변환(Viewport and canvas transforms) (0) | 2018.02.05 |
|---|---|
| 고도엔진 튜토리얼 #18 행렬과 변환(Matrices and transforms) (0) | 2018.02.05 |
| 고도엔진 튜토리얼 #16 커맨드라인 튜토리얼(Command line tutorial) (0) | 2018.02.03 |
| 고도엔진 튜토리얼 #15 유니티에서 고도엔진까지(From Unity3D to Godot Engine) (0) | 2018.02.03 |
| 고도엔진 튜토리얼 #14 2D와 3D 키바인딩(2D and3D keybindings) (0) | 2018.02.03 |