도입
이 튜토리얼를 읽기 전에 벡터 수학과 연속적인 내용이기 때문에 벡터 수학에 대한 설명을 읽어보는 것이 좋습니다.
이 튜토리얼에서는 변환에 대해서 다룰 것이며 행렬에 대해 조금 다룰 것입니다(그렇게 깊은 탐구는 하지 않습니다).
변환은 대부분의 시간을 이동, 회전, 크기 조정을 조정하는 데에 대부분의 시간을 사용하므로 이들이 가장 높은 우선순위로 고려될 것입니다.
객체 좌표 시스템 (OCS)
우주선이 공간 어디엔가 있다고 생각해보세요. 고도에서 이 우주선을 움직이고 회전하는 건 쉬운 일입니다 :
좋습니다, 2D에서 위치와 각을 회전에 사용하는 것은 간단해보입니다. 하지만 우리는 여기까지 오면서 각을 사용하지 않았다는 것을 기억하세요 (추가적으로, 각은 3D에서조차 그렇게 유용하게 사용되지 않습니다).
이 시점에서 누가 이 우주선을 설계하였는지를 깨달아야 합니다. 2D로 그려진 Paint.net, Gimp, Photoshop, etc. 또는 3D DCC 툴인 블렌더, 맥스, 마야 등 으로 그려진 3D입니다.
설계되었을 때는 회전되어있지 않았을겁니다. 우주선은 그것만의 좌표시스템에서 설계되었겠죠.

이건 우주선의 머리가 좌표를 가지고, 꼬리 등은 또다른 좌표를 가진다는 것을 의미합니다. 이는 픽셀 (2D) 또는 정점 (3D)이 될 수 있습니다.
그럼 다시 공간 어딘가에 있는 우주선을 불러보죠 :
어떻게 그곳에 도착한거죠? 설계된 곳에서 어떻게 움직이고 회전해서 지금의 위치로 움직였죠? 답은... 변환입니다. 우주선은 원래의 포지션에서 변환되어 새로운 곳에 도착한 것이죠. 이게 우주선을 지금 보이는 곳에 있게 한 것입니다.
하지만 변환이라는 건 너무 이 프로세스를 설명하기에는 일반적인 용어입니다. 이 수수께끼를 풀기 위해서, 원래 설계 위치와 지금 위치를 겹쳐놓을 것입니다 :
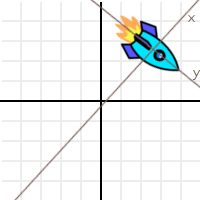
그래서, 우리는 "설계 공간"이 어떻게 이동했는지를 볼 수 있습니다. 이 변환을 어떻게 해야 제일 잘 나타낼 수 있을까요? 이를 위해 세 벡터를 사용할 겁니다(2D에서). X의 양으로 향하는 단위 벡터, Y의 양과 이동을 가리키는 단위 벡터.
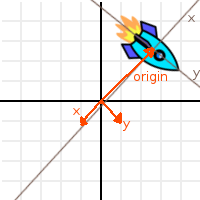
이 세 벡터를 "X", "Y", "Origin"이라고 부르고, 우주선에 겹쳐서 그리면 조금 더 말이 될 것 같네요 :
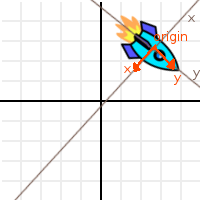
좋아요, 조금 나아졌지만 아직 잘 이해가 되지 않습니다. X, Y와 Origin이 어떻게 우주선을 여기 데려다 놓은거죠?
흠, 우주선의 위쪽 끝을 참조해서 이 점을 알아보죠 :
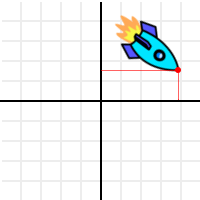
그리고 아래의 연산을 적용해 봅시다 (그리고 우주선의 모든 점에게도요, 하지만 우리는 참조된 우주선의 머리 끝만 쫓습니다).
var new_pos = pos - origin
이렇게 함으로써 선택된 점이 중앙으로 이동합니다 :
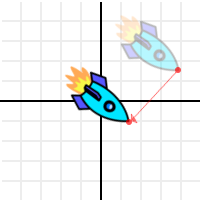
기대된 행동이지만, 좀 더 흥미로운 걸 해봅시다. X의 점곱을 사용하고 그 점과 점곱한 Y의 점을 더하는 겁니다 :
var final_pos = x.dot(new_pos) + y.dot(new_pos)
그럼 우리는 이런 걸 얻게됩니다.. 잠시만요, 우주선이 설계된 위치에 있습니다!
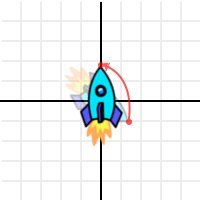
어떻게 이런 흑마법이 가능하죠? 공간에서 우주선은 길을 잃었었는데, 이제 집에 돌어왔습니다!
이상해 보이겠지만, 많은 논리적인 근거를 가지고 있습니다. 우리가 벡터 수학에서 보았듯이 X축까지의 거리와 Y축까지의 거리가 계산되었다는 것을 기억하세요. 평면이나 방향에서 거리를 계산하는 것은 점곱의 하나의 사용법입니다. 이는 우주선의 모든 점에 대한 설계 좌표를 찾아오기에 충분합니다.
따라서 우리가 지금까지 작업해 온 것(X, Y, Origin과 함께)은 객체 좌표 시스템입니다*. X와 Y는 **기저(Basis)*이고 *원점(Origin)은 오프셋(offset)입니다.
기저(Basis)
우리는 원점이 무엇인지 알고있습니다. 변환이 끝나고 새로운 지점으로 가고 나서도 설계 좌표 시스템의 (0, 0)입니다. 이게 원점이라고 불리는 이유이며, 하지만 행렬에서는 이는 단지 새로운 위치의 오프셋입니다.
기저는 더 흥미롭습니다. 기저는 OCS에서 새롭게 변환된 위치로부터 X와 Y의 방향이 정해집니다. 이것이 2D와 3D에서 무엇이 변한 것인지 알려줍니다. 원점(오프셋)과 기저(방향)가 "이봐, 디자인의 원래 X축과 Y축이 여기있어, 이 방향을 가리키고 있어."라고 소통합니다.
그래서, 기저의 표현을 바꾸어봅시다. 두 벡터 대신 행렬을 사용해봅시다.
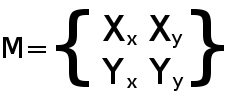
벡터는 행렬에 수평으로 있습니다. 다음 문제는.. 행렬이란 무엇일까요? 행렬에 대해 들어 본 적이 없을 것이라 생각합니다.
고도에서의 변환
이 튜토리얼에서는 행렬 수학(및 그 연산)을 심도 있게 설명하지 않고, 실제 실용적인 사용법만 설명합니다. 이에 대한 자료가 많이 있으며, 이 튜토리얼을 마친 후에는 훨씬 더 이해하기 쉬울 것입니다. 어떻게 변환을 샤용하는지만 설명할 것입니다.
행렬32
var m = Matrix32() var x = m[0] # 'X' var y = m[1] # 'Y' var o = m[2] # 'Origin'
대부분의 연산은 이 데이터타입(행렬32)와함께 설명됩니다. 3D에서도 같은 논리가 사용됩니다.
단위(identity)
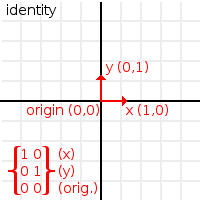
기본적으로 행렬 32는 "단위" 행렬로 만들어 졌습니다. 뜻하는 바는 :
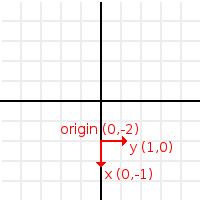
- 'X'의 오른쪽 점 : Vector2(1,0)
- 'Y'의 위쪽 점 (또는 픽셀에서의 아래) : Vector2(0,1)
- '원점'은 원점 벡터2(0, 0)입니다.
연산
회전
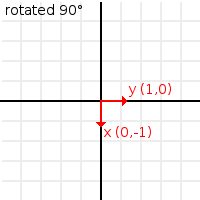
"회전" 함수를 이용해 행렬32를 회전할 수 있습니다 :
var m = Matrix32() m = m.rotated(PI/2) # rotate 90°
이동
두 가지 방법으로 행렬32를 이동할 수 있습니다. 첫번째는 원점을 움직이는 것입니다 :
# Move 2 units to the right var m = Matrix32() m = m.rotated(PI/2) # rotate 90° m[2]+=Vector2(2,0)
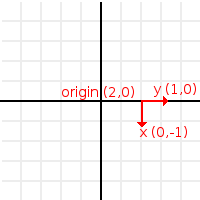
전역 좌표에서 항상 작동합니다.
대신, 행렬의 지역 좌표가 필요할 때 (기저가 시작된 곳으로) Matrix32.translated() 메소드가 있습니다 :
# Move 2 units towards where the basis is oriented var m = Matrix32() m = m.rotated(PI/2) # rotate 90° m=m.translated( Vector2(2,0) )
크기 변환
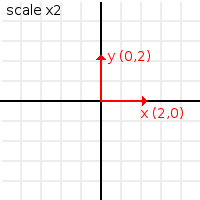
행렬은 크기 변환을 할 수도 있습니다. 스케일링은 기저 벡터에 벡터를 곱하면 됩니다(X 벡터는 스케일의 x 구성요소, Y 벡터는 스케일의 y 구성요소). 이건 원점을 건드리지 않습니다 :
# Make the basis twice its size. var m = Matrix32() m = m.scaled( Vector2(2,2) )
행렬 형태의 이러한 연산은 누적의 형태를 띕니다. 즉, 모든 것은 이전 것과 연관이 있다는 것입니다. 이 행성에서 오랫동안 산 사람들에게, 변환이 어떻게 작용하는지에 대한 좋은 참조는 다음과 같습니다 :

거북이와 비슷한 행렬입니다. 이 거북이는 아마도 안에 행렬을 가지고 있을 것입니다(여러분은 산타가 진짜가 아니라는 것을 배우는 데 오랜 시간이 걸렸을 것입니다).
변환
변환은 좌표 시스템 간에 전환하는 행동입니다. "디자이너(designer)" 좌표 시스템에서 OCS로 위치를 변환하기 위해서는 (2D나 3D나) "xform" 메소드가 사용됩니다.
var new_pos = m.xform(pos)
오직 기저를 위한 것입니다 (이동 없이) :
var new_pos = m.basis_xform(pos)
나중에 곱하는 것도 유효합니다 :
var new_pos = m * pos
역 이동
부정 연산을 할 때 (로켓이 위에 있을 때 우리가 하는 것처럼), "xform_inv" 메소드가 사용됩니다 :
var new_pos = m.xform_inv(pos)
기저만을 위해 :
var new_pos = m.basis_xform_inv(pos)
사전 곱셈을 위해 :
var new_pos = pos * m
직교 행렬
하지만 행렬이 크기 변환 되었을 때(벡터는 단위 벡터가 아닙니다)나 기저 벡터가 직교(90도)하지 않으면 역 변환은 작동하지 않습니다.
다르게 말하면, 역변환은 오직 직교 행렬일 때만 유효합니다. 이를 위해, 이러한 겨우엥는 아핀 역(affine inverse)이 계산되어야 합니다.
단위 행렬의 변환이나 역변환은 바뀌지 않은 위치를 반환합니다 :
# Does nothing, pos is unchanged pos = Matrix32().xform(pos)
아핀 역(Affine inverse)
아핀 역은 행렬이 또 다른 행렬의 역 연산을 하거나 행렬에 스케일을 하건 축 벡터가 직교하지 않든 상관이 없습니다. 아핀 역은 affine_inverse() 메소드를 사용해서 계산됩니다.
var mi = m.affine_inverse() var pos = m.xform(pos) pos = mi.xform(pos) # pos is unchanged
만약 행렬이 직교하면 :
# if m is orthonormal, then pos = mi.xform(pos) # is the same is pos = m.xform_inv(pos)
행렬 곱
하지만 규칙에 따라, 곱셈은 역순으로 합니다.
예 :
var m = more_transforms * some_transforms
더 명확하게 하기 위해서 :
pos = transform1.xform(pos) pos = transform2.xform(pos)
이는 다음과 같습니다 :
# note the inverse order pos = (transform2 * transform1).xform(pos)
하지만, 다음은 같지 않습니다 :
# yields a different results pos = (transform1 * transform2).xform(pos)
행렬 수학에서 A + B는 B + A와 같지 않습니다.
역에 의한 곱셈
행렬에 역행렬을 곱하면, 단위 행렬이 됩니다.
# No matter what A is, B will be identity B = A.affine_inverse() * A
단위 행렬에 의한 곱셈
행렬에 단위 행렬을 곱하면 행렬은 변하지 않습니다 :
# B will be equal to A B = A * Matrix32()
행렬 팁들
변환 계층 구조를 사용할 때는 행렬 곱셈이 역순이라는 것을 기억하세요! 계층 구조에 대한 전역 변환을 얻으려면 다음을 수행하세요 :
var global_xform = parent_matrix * child_matrix
세 단계로 :
# due to reverse order, parenthesis are needed var global_xform = gradparent_matrix + (parent_matrix + child_matrix)
부모를 기준으로 행렬을 만들려고 하면, 아핀 역함수(또는 정규 직교 행렬에 대한 정규 역원)를 사용합니다.
# transform B from a global matrix to one local to A var B_local_to_A = A.affine_inverse() * B
위의 예와 같이 되돌립니다 :
# transform back local B to global B var B = A * B_local_to_A
좋아요, 이것으로 충분합니다! 3D 행렬로 이동해서 튜토리얼을 완성해 보겠습니다.
3D에서의 행렬과 변환
앞에서 언급했듯이 3D의 경우 회전 행렬에 대해 3개의 Vector3 벡터를 처리하고 원점에 대해 추가로 하나씩 처리합니다.
행렬3(Matrix3)
고도는 행렬3이라는 특별한 형태의 3x3 행렬이 있습니다. 3D 회전 및 크기 변화를 나타내는 데 사용할 수 있으며 하위 벡터는 다음과 같습니다 :
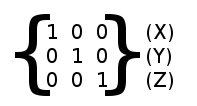
var m = Matrix3() var x = m[0] # Vector3 var y = m[1] # Vector3 var z = m[2] # Vector3
또는 이렇게 대체할 수 있습니다 :
var m = Matrix3() var x = m.x # Vector3 var y = m.y # Vector3 var z = m.z # Vector3
행렬3은 기본적으로 단위 행렬로 초기화됩니다.
3D에서의 회전
3D에서의 회전은 2D에서의 회전(이동과 크기 변환도 같습니다)보다 복잡하기 때문에 회전은 암시적인 2D 작업으로 처리됩니다. 3D에서 회전하려면, 축을 선택해야 합니다. 그러면 이 축을 중심으로 회전이 발생합니다.
회전 축은 단위 벡터여야 합니다. 벡터가 어떤 방향을 가리킬 수 있는 것과 같지만 길이는 (1, 0)이어야 합니다.
#rotate in Y axis var m3 = Matrix3() m3 = m3.rotated( Vector3(0,1,0), PI/2 )
변환
최종 구성 요소를 다 섞기 위해, 고도는 변형 유형을 제공합니다. 변환에는 두 멤버가 있습니다 :
var t = Transform() pos = t.xform(pos) # transform 3D position pos = t.basis.xform(pos) # (only rotate) pos = t.origin + pos (only translate)
'레퍼런스 > 고도엔진' 카테고리의 다른 글
| 고도엔진 튜토리얼 #20 캔버스 층(Canvas layer) (0) | 2018.02.05 |
|---|---|
| 고도엔진 튜토리얼 #19 뷰포트와 캔버스 변환(Viewport and canvas transforms) (0) | 2018.02.05 |
| 고도엔진 튜토리얼 #17 벡터 수학(Vector math) (0) | 2018.02.05 |
| 고도엔진 튜토리얼 #16 커맨드라인 튜토리얼(Command line tutorial) (0) | 2018.02.03 |
| 고도엔진 튜토리얼 #15 유니티에서 고도엔진까지(From Unity3D to Godot Engine) (0) | 2018.02.03 |